SUDUT ANTAR VEKTOR PADA BIDANG BERDIMENSI DUA DAN BERDIMENSI TIGA BERSAMA CONTOH SOALNYA
Vektor matematika tak hanya terdiri dari beberapa jenis saja, namun vektor matematika juga terdiri dari beberapa macam.
Nah beriktu akan kami berikan macam-macam vektor beserta dengan operasinya sekaligus, simak baik-baik ya:
Vektor di R2
Panjang dari suatu segmen garis yang menyebutkan vektor dilambangkan dengan memakai 
atau dapat juga dinotasikan dengan menggunakan simbol ||
Berikut ini panjang dari vektor yaitu seperti berikut ini:
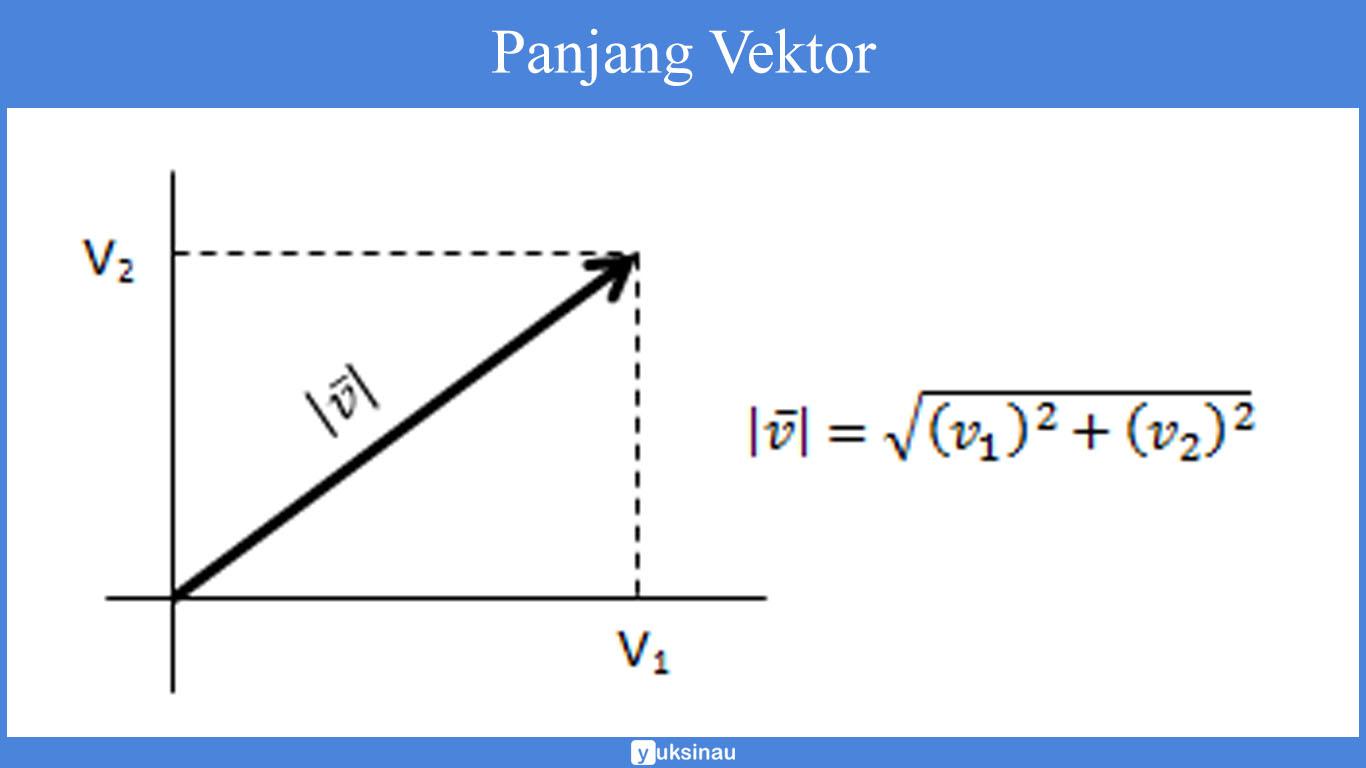
Panjang vektor sendiri adalah bentuk yang bisa dihubungkan dengan sudut ∅ yang dapat dengan mudah untuk dibentuk oleh vektor serta juga sumbu positif.
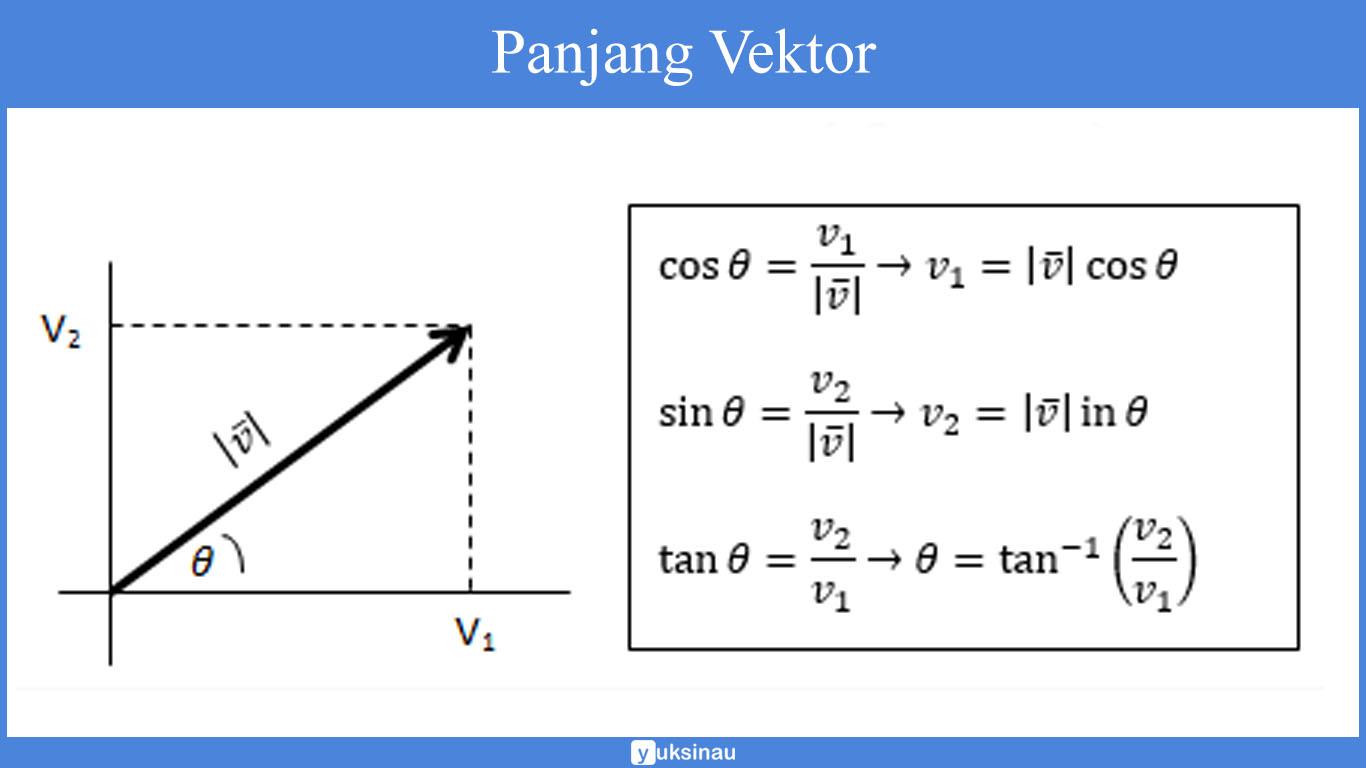
Operasi Vektor di R2
⇒ Proses penjumlahan dan juga Pengurangan Vektor di R2
Resultan adalah sebutan dari hasil penjumlahan yang dilakukan pada dua vektor atau pun lebih.
Penjumlahan pada vektor ini sendiri juga dapat dilakukan secara aljabar serta juga dapat dilakukan dengan memakai cara menjumlahkan komponen yang berada di posisi sama atau seletak.
Apabila:
maka :
Maka penjumlahan secara grafis sendiri dapat kita lihat pada contoh gambar yang ada di bawah ini:
Pada pengurangan vektor ini diberlakukan sama dengan yang ada pada penjumlahan, antara lain adalah sebagai berikut, lihat pada contoh di bawah ini:
Sifat -sifat di dalam penjumlahan vektor ini sendiri adalah seperti di bawah ini, silahkan disimak rumusnya:
⇒ Perkalian Vektor di R2 Dengan Skalar
Suatu vektor sendiri juga dapat dikalikan dengan suatu skalar atau bilangan real yangnantinya akan menghasilkan suatu vektor baru jika adalah vektor dan k merupakan skalar.
Sehingga perkalian vektor dapat dinotasikan menjadi seperti di bawah ini:
Berikut ini merupakan beberapa keterangan selengkapnya:
- Apabila k > 0, maka vektor akan searah dengan vektor
- Apabila k < 0, maka vektor akan berlawanan arah dengan vektor
- Apabila k = 0, maka vektor merupakan vektor identitas
.
Jika secara grafis perkalian ini dapat mengubah panjang vektor serta dapat dilihat pada tabel yang terletak di bawah ini:
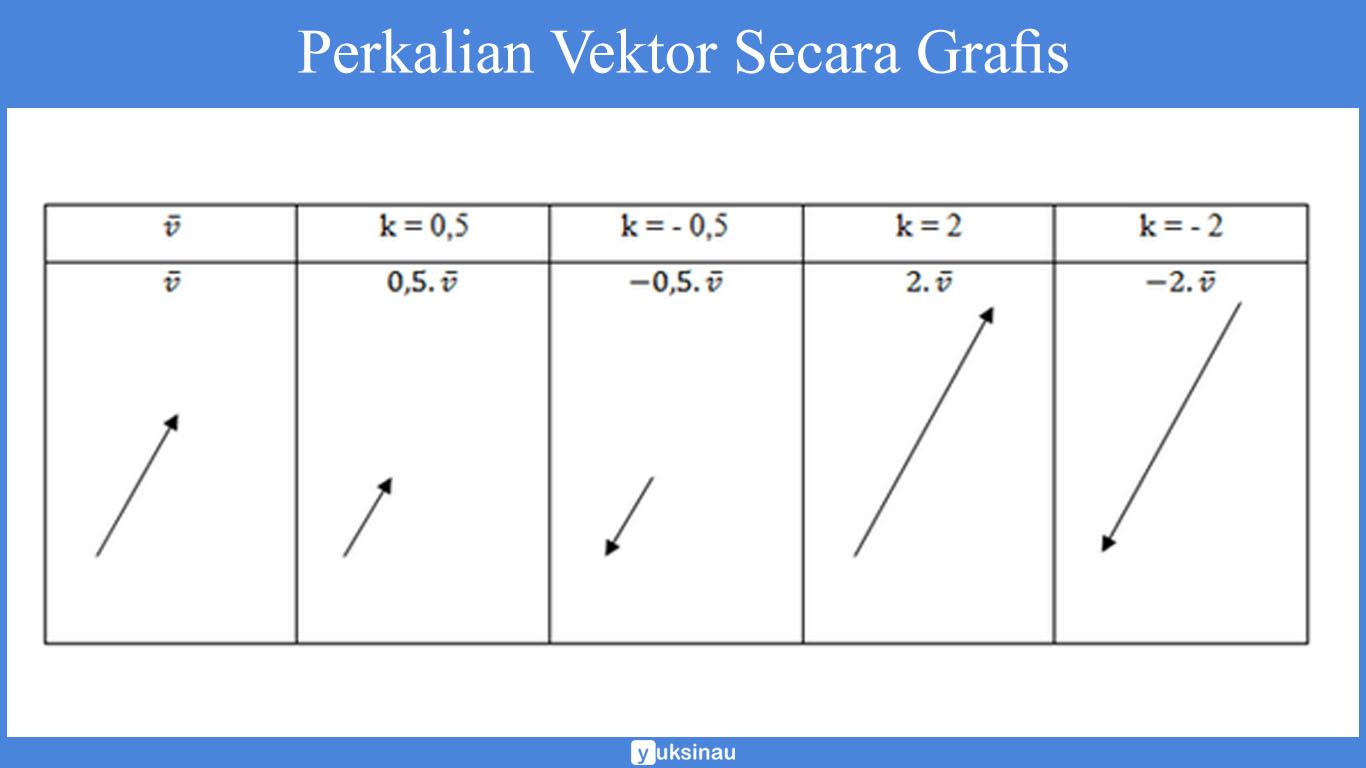
Jika secara aljabar, perkalian vektor
⇒ Perkalian Skalar Dua Vektor di R2
Dalam perkalian skalar dua vektor bisa juga disebut sebagai hasil kali titik dua vektor yang dapat kita tuliskan seperti yang ada di bawah ini:
Vektor di R3
Vektor yang terelta di dalam ruang tiga dimensi (x, y, z) di mana jarak antara dua titik vektor dalam R3 bisa kalian ketahui dengan pengembangan rumus phytagoras.
Apabila titik dari A(x2. y2. z2) serta B(x2. y2. z2) adalah:
Atau apabila 
, sehingga:
Vektor 
bisa disebutkan dalam dua bentuk, yakni dalam kolom
atau dalam baris menjadi 
Vektor juga bisa disajikan sebagai kombinasi linier dari vektor basis seperti 
atau 
dan atau 
berikut selengkapnya:
Operasi Vektor di R3
Operasi vektor di R3 secara umum, mempunyai konsep yang sama dengan operasi yang ada di vektor R2 dalam penjumlahan, pengurangan, hingga perkalian.
Penjumlahan dan pengurangan vektor di R3
Penjumlahan dan juga pengurangan vektor di R3 sama dengan yang ada di vektor R2 yakni:
Perkalian vektor di R3 dengan skalar
Apabila
Hasil kali skalar dua vektor
Selain rumus pada R3, terdapat rumus lain dalam hasil kali skalar dua vektor. Apabila 
dan 
maka 
adalah:
Contoh Soal
1. Diketahui titik-titik A (3,-1,0), B(2,4,1) dan C(1.0,5). Maka panjang proyeksi vektor AB pada vektor BC adalah...
A. 1/5 √30
B. 2/5 √30
C. 3/5 √30
D. 4/5 √30
E. √30
Pembahasan
AB = B - A = (2,4,1) - (3,-1,0) = (-1,5,1)
AC = C - A = (1,0,5) - (3,-1,0) = (-2,1,5)
Maka panjang proyeksi vektor AB pada vektor BC adalah...
= 12/30 (√30) = (2/5) √30
Jawaban: B
2. Vektor-vektor u = 2i - mj + k dan v = 5i + j - 2k saling tegak lurus. Maka harga m haruslah...
A. 2
B. 4
C. 6
D. 8
E. 10
Pembahasan
u tegak lurus v maka:
u . v = 0
(2i - mj + k) (5i + j - 2k) = 10 - m - 2 = 0
m =8
Jawaban:D
3. Diketahui D adalah titik berat segitiga ABC dimana A(2,3,-2), B(-4,1,2) dan C(8,5,-3). Maka panjang vektor posisi d sama dengan:
A. 1
B. 2
C. √5
D. √10
E. √14
Pembahasan
D titik berat segitiga sehingga D = 1/3 (A + B + C)
D = 1/3 (2,3,-2) + (-4,1,2) + (8,5,-3)
D = 1/3 (6,9,-3) = (2,3,-1)
Panjang proyeksi D adalah
Jawaban: E
4. Jika titik-titik P, Q, R segaris dan P(-1,1) dan R (3,5) dan PQ = QR maka titik Q adalah...
A. (3,1)
B. (1,3)
C. (1,1)
D. (3,3)
E. (-3,-1)
Pembahasan
PQ = QR maka Q - R = R - Q
2Q = R + P
Q = 1/2 (R + P)
Q = 1/2 (3,5) + (-1,1) = 1/2 (2,6) = (1,3)
Jawaban: B
5. Diketahui A (1,2,3), B(3,3,1) dan C(7,5,-3). Jika A, B, dan C segaris, perbandingan AB : BC =...
A. 1 : 2
B. 2 : 1
C. 2 : 5
D. 5 : 7
E. 7 : 5
Pembahasan
AB = B - A = (3,3,1) - (1,2,3) = (2,1,-2)
Besar AB = √22 + 12 + (-2)2 = 3
BC = C - B = (7,5,-3) - (3,3,1) = (4,2,-4)
Besar BC = √42 + 22 + (-4)2 = 6
Jadi perbandingan AB : BC = 3 : 6 = 1 : 2
Jawaban: A
